4) An Overview on Logistic Regression in ML

 An Overview on Logistic Regression in ML

Introduction:

                               This is a supervised ML algorithm and also known to solve the binary classification problems. Binary means two and classification means natures and this means that we use it, to predict the nature between two natures.  In simple words here we have two classes it can be true(presence) or false(absence) or may be 1 or 0,  Like Linear Regression problem which we discussed in blog 4, we give and input x and model (discuss it later) will predict output y. In of the point is false categories called negative class and true categories called positive class.

How to achieve Logistic Regression:

                             To Achieve logistic regression we use sigmoid function which gives us the value of 0 and 1. We apply condition here to get the prediction in 0 and 1 form like if f(x) which is output greater than 0.5 then real output will be 1 and if less than 0.5 then real output will be 0. This we cannot achieve if we start using the linear function for this kind of problem also like linear regression problems because linear function can give us the output in wide variety of numbers which can make difficult to get classification number like 0 and 1. 

Sigmoid Formula:

               

An overview of Logistic Regression with single neuron:

As you can see x is input which will multiply by weight(w) and add by bias(b) and sigma is activation

function sigmoid after applying sigmoid we will get the output y. Here after getting the output y we will compare thus output with the actual output if both are same or close then good we test this thing using the loss function if loss is less then good otherwise we will change the value of weights and bias using gradient decent. This we will do until we reach the closest value.

Loss Function Formula:

                         L(f w[ i ] ,b ) ,y1 ) =- ( yi ) log ( fwb ( x[i] ) ) - ( 1 - yi ) log ( 1 - fw[i] , b ( x[i] ) )

Cost Function Formula (Gradient Decent Formula):

                         J ( w[i] , b ) = 1 / m ( sigma ( L ( fw [i] , b ( x[i] , yi ) ) )

Notes:

Code:

from distutils.log import warn
import numpy as np
import matplotlib.pyplot as py
x_train=np.array([2,3,5,6,9,1])
y_train=np.array([0,0,1,1,1,0])
np.seterr(divide = 'ignore') 
# np.seterr(divide='warn')
def calculate(x,w,b):
    fx=np.dot(x,w)+b
    return fx
def sigmoid(z):
    fx=1/(1+2.71**(-z))
    return fx
def cost(x,y,w,b):
    m=len(x)
    t_cost=0
    sum_cost=0
    for i in range(m):
        fx=sigmoid(np.dot(x[i],w)+b)
        print("here is the issue ",fx)
        t_cost=-(x[i]*np.log(fx))-((1-x[i])*np.log(1-fx))
        sum_cost+=t_cost
    total_cost=(1/m)*sum_cost
    return total_cost
def gradientLoss(x,y,w,b):
    m=len(x)
    lossW=0
    lossB=0
    sum_loss_w=0
    sum_loss_b=0
    historyW=np.zeros(m)
    historyB=np.zeros(m)
    for i in range(m):
        fx=sigmoid(np.dot(x[i],w)+b)
        loss=fx-y[i]
        lossW=loss*x[i]
        lossB=loss
        historyW[i]=lossW
        historyB[i]=lossB
        sum_loss_w+=lossW
        sum_loss_b+=lossB
    sum_loss_w=(1/m)*sum_loss_w
    sum_loss_b=(1/m)*sum_loss_b
    return sum_loss_w,sum_loss_b

def gradient(x,y,w,b,lr,iterations):
    historyW=np.zeros(iterations)
    historyB=np.zeros(iterations)
    for i in range(iterations):
        gradientW,gradientB=gradientLoss(x,y,w,b)
        w=w-(lr*(gradientW))
        b=b-(lr*(gradientB))
        historyW[i]=w
        historyB[i]=b
    return historyW,historyB
def predict(x,w,b):
    result=np.zeros(len(x))
    for i in range(len(x)):
        output=calculate(x_train[i],w,b)
        if(output>0):
            result[i]=1
        else:
            result[1]=0
    return result    
        
    
w=0.1
b=1
lr=0.1
historyW,historyB=gradient(x_train,y_train,w,b,lr,1000)
print("Weights are ",historyW)
print("Bias are ",historyB)
w=historyW[-1]
b=historyB[-1]
# total_cost=cost(x_train,y_train,w,b)
# print("Cost is ",float(total_cost))

output=predict(x_train,w,b)
print("Output is ",output)
output2=sigmoid(np.dot(x_train,w+b))
print("Sigmoid output is ",output2)
py.scatter(output,output2,c='r')
py.title("Comparison")
py.xlabel("predict")
py.ylabel("sigmoid")
py.show()

    

    
    

Read More

More operators, order, between, in, like and where clause

 

In this blog we will talk about some more operators which we can use in oracle SQL e.g not, or, and, >=, <=, <, >, =, <> etc. These are some more operators and how we can use them now we will understand this.

Before learning about these operators we should understand about where clause. As this name is showing the qualities of this clause that it uses when we want to filter the result also this we can use only with the select statement. Example to use this clause is given below

select ename from emp where empid=2;

Meaning: Meaning of this query is to find the employee name from employee table where employee if is equal to 2.

Use of the operators:

select ename, sal from emp where sal>2000;

select ename, sal from emp where sal<2000;

select ename, sal from emp where sal>=2000 or sal<=2000;

select ename, sal from emp where sal<>1000; (Not equal to operator)

This is how we can use these operators. There are also lot of the things which we can perform in oracle SQL.

Order:

We can also show the result in ascending or descending order and how we can use this is given below

select ename, sal from emp order by ename asc; (result will show alphabetically) 

select ename, sal from emp order by ename desc; (result will be show in descending order)

You can also check the result by copy the query and paste that queries to the SQL plus. 

Between, in, like:

As the name showing the meaning that between is uses to show the result between two inputs, In uses as or operator and like is uses to show the similar result for like. How we can use this examples are given below

1) select ename, sal from emp where sal between 1000 and 500; (this will show the salaries which are between 1000 and 500)

2) select ename, sal from emp where empid in(1,2,3); (this will show the ename and salaries for empid's which are 1, 2 or 3;

3) select * from emp where ename like'%R'; (this will show the results where enames end with R)

More about Like:

There are more things which are necessary to understand about the like operator so there are below

like'%R%'; (this will display the result for enames where names contain R in the center)

Read More

3) Multiple Linear Regression

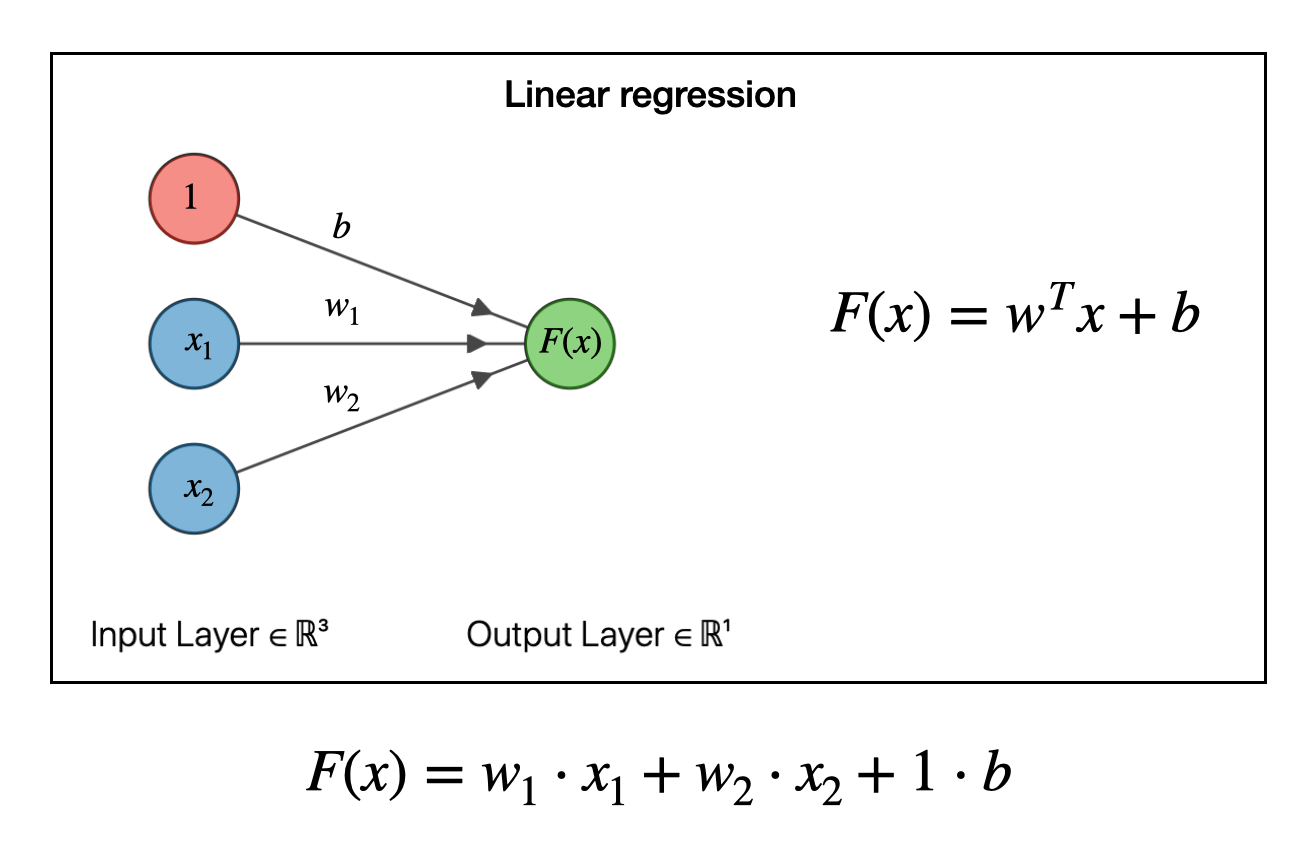
 Multiple Linear Regression

Here we have multiple features such as (x1,x2,x3...) instead of one feature (x1) and after feed these features to model we can get the output (y). Before proceeding away we should understand some of the terminologies which we use for ML. let's assume a[i][j] here will the help of j we can proceed toward columns and with the help of i we can proceed toward rows. Furthermore, n is the total number features.

How Model find value for Multiple Features:

let’s assume we have 3 features x1, x2 and x3 with three weights w1, w2, w3 and one bias b and by using these values we can find the output f(x).

f(x)= ((x1*w1)+(x2*w2)+(x3*w3))+b

After getting the f(x) value we go ahead by finding the loss with the help of loss function and apply gradient decent to get the right parameters (weight and bias) for the model. This all we will understand with time. But for now we should have little bit of understanding for basic terminologies, methods and approaches.

=> We have bias b, weights [w1,w2,w3..] and features [x1,x2,x3…]

=> Model f(x)= pred_y[ i ] =w1*x1+w2*x2+…+w(n)*x(n)

=> cost function J(w[i],b)=((sigma(pred_y[i]- actual_y[i]))²)/2m

=>update weight w[i]= w[i]- learning rate * ( J(w[i], b ) * x[i]

=>update bias b= b- learning rate * (J(w[i],b)

Note: Vectorization is good approach to perform any operation as compare to use loops

Here we have Model named as f(x) and with the help of model we predict our output (y). After predicting the value (y) we will find the error using cost function called Gradient decent. Our parameters will perfectly tuned if our cost function is close to zero. With the help of cost function we will find the cost between actual_y (output) and predicted_y (output). If our error is high then we will update the weight and bias and make the cost close to 0.

Feature Scaling:

In simple word this is normalization of independent features. This helps us make gradient fast. We use normalization if either feature difference is too small or too large. Therefore, in normalization we scale the values between 0 and 1 most of the case. We can take the example of images while training model for images we normalize the images to make training fast for model. There are too much types of normalization and mostly common two of them are given below

1) Z-Score Normalization: Here data (features) will normalize in such that mean of your data will be zero and standard derivation will become 1.

               Formula:          x1= ( x1 - mean( u1 ) ) / ( standard deviation )

2) Mean Normalization:   Here we normalize the data with respect to mean

             

               Formula:           x1= ( x1 - mean( u1 ) ) / ( max - min )

Note: Now a days features engineering is one of the most useful thing in ML because with the help of it we identifies news features for model

An overview Diagram of Linear Regression:

Notes for Linear Regression:

I made very simplified version linear regression Code (Python) which is given below:

import numpy as np
import matplotlib.pyplot as plt
xFeatures=np.array([2,3])
yFeatures=np.array([330,400])
# plt.scatter(xFeatures,yFeatures,marker='x',c='r')
# plt.title("Actual Values")
# plt.xlabel("Size")
# plt.ylabel("Price")
# plt.show()
lr=0.1
m=len(xFeatures)
def calculate(x,w,b):
    y=w*x+b
    return y
def cost(x,y,w,b):
    JSumWeight=0
    m=len(x)
    for i in range(m):
        f_wb=(w*x[i])+b
        JSumWeight=JSumWeight+np.power((f_wb-y[i]),2)
    totalCostW=(1/2*m)*JSumWeight
    return totalCostW

def gDecent(x,y,w,b):
    wid=0
    bs=0
    sumWeights=0
    sumBias=0
    for i in range(len(x)):
        f_wb=(w*x[i])+b
        wid=(f_wb-y[i])*x[i]
        bs=(f_wb-y[i])
        sumWeights+=wid
        sumBias+=bs
        
    sumWeights=(1/m)*(sumWeights)
    sumBias=(1/m)*(sumBias)
    return sumWeights,sumBias
            
def resultGDecent(x,y,w,b,iterations):
    recordW=np.zeros(iterations)
    recordB=np.zeros(iterations)
    for i in range(iterations):
        errorW,errorB=gDecent(x,y,w,b)
        newW=w-(lr*errorW)
        newB=b-(lr*errorB)
        w=newW
        b=newB
        recordW[i]=w
        recordB[i]=b
    
    return recordW,recordB

bias=1
weight=0.25
w,b=resultGDecent(xFeatures,yFeatures,weight,bias,1000)
print("1st Weight is ",w)
print("1st Bias is ",b)

# w,b=resultGDecent(xFeatures,yFeatures,w,b)
# print("Last Weight is ",w)
# print("Last Bias is ",b)
# w,b=resultGDecent(xFeatures,yFeatures,w,b)
# print("Last 1 Weight is ",w)
# print("Last 1 Bias is ",b)
getCost=cost(xFeatures,yFeatures,w,b)
print("Cost is ",getCost)
# plt.scatter(w,b,marker='x',c='r')
# plt.title("Actual Values")
# plt.xlabel("Width")
# plt.ylabel("Height")
# plt.show()
print("Our real value is ",xFeatures*w[-1]+b[-1])

Output:
After updating weights and bias we will have predicted value below
Our predicted value (y) is [328.882757 400.78734259]
You can check the actual y above in the code. For features x our model is predicting these values y after updating weights and bias with the help of gradient decent.
For Now this is enough. Today we learn some of the terminologies and functions which helps us for training model and updating weights and bias. We also see the basic code for linear regression.

Read More